二叉搜索树的删除可以分为三种情况。第一,被删除的节点是叶子节点:
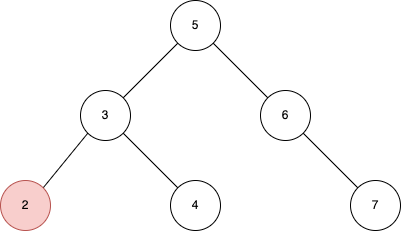
第二,被删除的节点只有一个孩子节点:
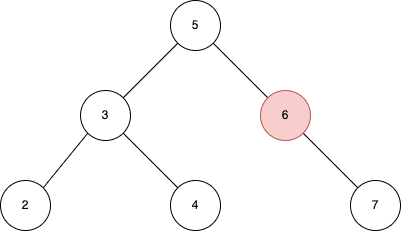
第三,被删除的节点有两个孩子节点:

对于第一种情况,我们只需断开被删除的节点和其父节点的关联即可,即将节点3的左孩子节点指针置为空;对于第二种情况,我们可以用被删除的节点的孩子节点来替代被删除的节点,即将节点5的右孩子指针改为指向节点7;第三种情况是最为复杂的情况,相当于删除一个子树的根节点,为了保持二叉搜索树的性质,我们可以使用左子树中的最大值或右子树的最小值来替代被删除的根节点。
不过在实现时,考虑到实现的简便,对于第三种情况会通过直接修改当前节点的值来替代修改节点的指针指向,以上述例子来说,如果使用指针修改的方式,则需要修改节点5的左孩子指针,修改节点2的左孩子指针和右孩子指针(这里假设使用节点2来替代被删除的节点3),总共三处修改较为繁琐;而如果使用修改节点值的方式,只需要先将节点3的值改为2(这里假设使用节点2来替代被删除的节点3),然后就可以将问题转化为在余下的左子树中删除节点2。具体代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def deleteNode(self, root: TreeNode, key: int) -> TreeNode:
if not root:
return root
if root.val < key:
root.right = self.deleteNode(root.right, key)
elif root.val > key:
root.left = self.deleteNode(root.left, key)
else:
if root.left and root.right:
root.val = self._find_min(root.right)
root.right = self.deleteNode(root.right, root.val)
else:
return root.left or root.right
return root
def _find_min(self, root):
while root.left:
root = root.left
return root.val
|


